Презентация на тему доказательство теоремы пифагора. Проект-презентация "Теорема Пифагора и способы её доказательства" Доказательство теоремы пифагора готовые презентации

Основные задачи Рассмотреть биографию Пифагора Познакомиться с его школой Собрать исторические сведения о теореме Исследовать различные способы доказательства теоремы Пифагора Рассмотреть исторические и практические задачи на применение теоремы Пифагора

Пифагор Самосский (ок ок. 500 г. до н.э.) Пифагор и его школа Пифагор родился около 580 г. до н.э. на греческом острове Самосе. Получил хорошее образование. В Греции он организовал свою школу, которая действовала почти 30 лет, её раньше называли пифагорейским союзом. Пифагор не оставил после себя собраний сочинений, он держал всё в тайне и передавал ученикам устно. Самое большее, что известно сейчас – это теорема Пифагора.

История теоремы Пифагора Исторический обзор начинается с древнего Китая. Египтяне строили прямые углы при помощи таких треугольников, используя натягивание верёвки. В древнем Вавилоне в 2000 г. до н.э. проводили приближённое вычисление гипотенузы прямоугольного треугольника. Теорема Пифагора обнаружена в папирусе времён фараона Аменемхета и вавилонских клинописных табличках VII-V в. до н.э. Сегодня принято считать, что Пифагор дал первое доказательство носящей его имя теоремы, но оно не сохранилось.

Доказательство Евклида Дано: Δ ABC - прямоугольный Доказать: S ABFH + S ACKG = S BCED. Доказательство: AO- высота, опущенная на гипотенузу. Докажем, что её продолжение делит построенный на гипотенузе квадрат на два прямоугольника, площади которых равны площадям соответствующих квадратов, построенных на катетах. Докажем, что прямоугольник BOLD равновелик квадрату ABFH. Δ ABD=ΔBFC (по двум сторонам и углу между ними BF=AB; BC=BD; угол FBC = углу ABD). S Δ ABD=1/2 S прямоугольника BOLD, т.к. у ΔABD и прямоугольника BOLD общее основание BD и общая высота LD. АНАЛОГИЧНО, S ΔFBC=1/2 S прямоугольника ABFH (BF-общее основание, AB-общая высота). Отсюда, учитывая, что S Δ ABD = S ΔFBC, имеем: S BOLD=S ABFH. АНАЛОГИЧНО, используя равенство Δ BCK и Δ ACE, доказывается, что S OCEL= S ACKG. S ABFH + S ACKG = S BOLD + S OCEL = S BCED. O

Доказательство методом площадей Дано: abc – прямоугольный треугольник Доказать: c 2 = a 2 + b 2 Доказательство: Расположим четыре равных прямоугольных треугольника так, как показано на рисунке. Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол 180°. Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата. Что и требовалось доказать

Построим ΔABC с прямым углом С. Доказательство Гофмана A B C a b c F D E Построим BF=CB, BF CB Построим BE=AB, BE AB Построим AD=AC, AD AC Точки F, C, D принадлежат одной прямой. Как мы видим, четырёхугольники ADFB и ACBE равновелики, т.к. ΔABF= ΔЕCB. Треугольники ADF и ACE равновелики. Отнимем от обоих равновеликих четырёхугольников общий для них ΔABC, получим: 1/2 а 2 +1/2b 2 =1/2 с 2 Соответственно: а 2 + b 2 =с 2

Доказательство Вальдхейма Дано: прямоугольный треугольник с катетами a и b, гипотенузой - c Доказать: a²+b²=c² Доказательство: Выразим площадь трапеции двумя путями. Sтрапеции = (a+b)²/2 Sтрапеции = ab + c²/2 При ревнивая правые части получим: a²+b²=c² Теорема доказана.

Векторное доказательство Дано: АВС - прямоугольный треугольник с прямым углом при вершине С, построенный на векторах СВ и СА Доказать: c² = a² + b² Доказательство: Справедливо векторное равенство: b + c = a, откуда имеем c = a – b, возводя обе части в квадрат, получим c² = a² + b² - 2a b Так как СВ перпендикулярно СА, то a b = 0, откуда c² = a² + b² или c² = a² + b²

Исторические задачи Задача индийского математика 12 века Бхаскары: «На берегу реки рос тополь одинокий Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С течением реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка. Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?» Решение: пусть СD – высота тополя, DC=CB + BD, по теореме Пифагора имеем АС ² + СВ ² = АВ ², 3 ² + 4 ² = 25, АВ = 5 футов. CD = 3+5 = 8(футов) Ответ: 8 футов.

Древнеиндийская задача Над озером тихим С полфута размером Он рос одиноко. И ветер порывом Отнес его в сторону. Нет Боле цветка над водой. Нашёл же рыбак его ранней весной В двух футах от места, где рос. Итак, предложу я вопрос: Как озера вода здесь глубока? Какова глубина в современных единицах длины? Решение: Выполним чертёж к задаче и обозначим глубину озера DС =Х, тогда BD = AD = Х + 0,5. Из треугольника DCB по теореме Пифагора имеем CD² = DB² – CB². (Х + 0,5)² – Х² = 2², Х² + Х² + 0,25 – Х² = 4, Х = 3,75. Таким образом, глубина озера составляет 3,75 фута. 3, 75 0,3 = 1,125 (м) Ответ: 3,75 фута или 1, 125 м.

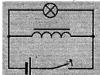
Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.) Решение: Пусть AB= x, BC=R=200 км, OC= r =6380 км. OB=OA+AB OB=r + x. Используя теорему Пифагора, получим ответ: 2,3 км.

Молниеотвод Известно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту. Решение: По теореме Пифагора h2 a2+b2, значит h(a2+b2)1/2.

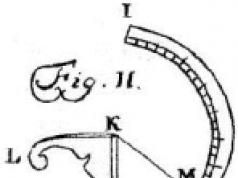
Окна В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг половине ширины, (b/2) для внутренних дуг Остается еще полная окружность, касающаяся четырех дуг. Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра.

В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p. По теореме Пифагора имеем: (b/4+p) ²=(b/4) ²+(b/2-p) ² или b²/16+ bp/2+p²=b²/16+b²/4-bp+p², откуда bp/2=b²/4-bp. Разделив на b и приводя подобные члены, получим: (3/2)p=b/4, p=b/6.

Астрономия На этом рисунке показаны точки A и B и путь светового луча от A к B и обратно. Путь луча показан изогнутой стрелкой для наглядности, на самом деле, световой луч - прямой. Какой путь проходит луч? Поскольку свет идет туда и обратно одинаковый путь, спросим сразу: чему равно расстояние между точками?

Строительство крыши При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки. Например: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м., и AB=BF. Решение: Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда: А) Из треугольника DBC: DB=2,5 м., Б) Из треугольника ABF:

Слайд 1

Теорема Пифагора
"Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку."

Слайд 2

Слайд 3

История теоремы
Исторический обзор начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чупей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: "Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4". В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.

Слайд 4

Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

Слайд 5

Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.

Слайд 6

Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой-на критическом изучении греческих источников,Ван-дер-Варден (голландский математик) сделал следующий вывод:

Слайд 7

Формулировка теоремы
« Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах» « Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».
Во времена Пифагора теорема звучала так:
или

Слайд 8

Современная формулировка
« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».

Слайд 9

Доказательства теоремы
Существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.).

Слайд 10

Самое простое доказательство
Рассмотрим квадрат, показанный на рисунке. Сторона квадрата равна a + c.
c
a

Слайд 11

В одном случае (слева) квадрат разбит на квадрат со стороной b и четыре прямоугольных треугольника с катетами a и c.
a
c
a
c
В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c.
a
c
Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.

Слайд 12

Доказательство Евклида
Дано: ABC-прямоугольный треугольник Доказать: SABDE=SACFG+SBCHI

Слайд 13

Доказательство:
Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного треугольника ABC, а ACFG и BCHI-квадраты, построенные на его катетах. Опустим из вершины C прямого угла перпендикуляр CP на гипотенузу и продолжим его до пересечения со стороной DE квадрата ABDE в точке Q; соединим точки C и E, B и G.

Слайд 14

Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что треугольники ACE и AGB(закрашенные на рисунке) равны между собой (по двум сторонам и углу, заключённому между ними). Сравним далее треугольник ACE и прямоугольник PQEA; они имеют общее основание AE и высоту AP, опущенную на это основание, следовательно SPQEA=2SACE Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит, SFCAG=2SGAB
Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.

Слайд 15

Алгебраическое доказательство
Дано: ABC-прямоугольный треугольник Доказать: AB2=AC2+BC2
Доказательство: 1) Проведем высоту CD из вершины прямого угла С. 2) По определению косинуса угла соsА=AD/AC=AC/AB, отсюда следует AB*AD=AC2. 3) Аналогично соsВ=BD/BC=BC/AB, значит AB*BD=BC2. 4) Сложив полученные равенства почленно, получим: AC2+BC2=АВ*(AD + DB) AB2=AC2+BC2. Что и требовалось доказать.

Слайд 16

Геометрическое доказательство
Дано: ABC-прямоугольный треугольник Доказать: BC2=AB2+AC2
Доказательство: 1) Построим отрезок CD равный отрезку AB на продолжении катета AC прямоугольного треугольника ABC. Затем опустим перпендикуляр ED к отрезку AD, равный отрезку AC, соединим точки B и E. 2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников:
SABED=2*AB*AC/2+BC2/2 3) Фигура ABED является трапецией, значит, её площадь равна: SABED= (DE+AB)*AD/2. 4) Если приравнять левые части найденных выражений, то получим: AB*AC+BC2/2=(DE+AB)(CD+AC)/2 AB*AC+BC2/2= (AC+AB)2/2 AB*AC+BC2/2= AC2/2+AB2/2+AB*AC BC2=AB2+AC2. Это доказательство было опубликовано в 1882 году Гэрфилдом.

Слайд 17

Значение теоремы Пифагора
Теорема Пифагора- это одна из самых важных теорем геометрии. Значение её состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии.

Слайд 18

В средние века теорема Пифагора, magister matheseos, определяла границу если не наибольших возможных, то по крайней мере хороших математических знаний. Характерный чертёж теоремы Пифагора, который ныне иногда превращается школьниками, например, в облаченного в мантию профессора (рис. 7, 8) или в человечка в цилиндре (рис. 9) и т.п., в те времена всеобщей страсти к символам нередко употреблялся как символ математики. Столь же часто мы встречаемся с «Пифагором» в средневековой живописи, мозаике, геральдике.

Чернов Максим

Проект по геометрии, оформленный в виде презентации на тему "Теорема Пифагора и различные способы её доказательства"

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Теорема Пифагора и различные способы её доказательства Выполнил: Чернов Максим 8А

Цель проекта: Изложить теорему Пифагора, представить разные способы её доказательства.

История В древнекитайской книге Чжоу би суань цзин говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары. Мориц Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам ещё около 2300 г. до н.э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора, гарпедонапты, или « натягиватели верёвок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Очень легко можно воспроизвести их способ построения. Возьмём верёвку длиною в 12 м и привяжем к ней по цветной полоске на расстоянии 3 м от одного конца и 4 метра от другого. Прямой угол окажется заключённым между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становится излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, - например, рисунки, изображающие столярную мастерскую. Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммурапи, то есть к 2000 г. до н.э., приводится приближённое вычисление гипотенузы равнобедренного прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой - на критическом изучении греческих источников, Ван-дер- В арден (голландский математик) сделал вывод о большой вероятности того, что теорема о квадрате гипотенузы была известна в Вавилоне уже около XVIII века до н. э. Согласно комментарию Прокла к Евклиду, Пифагор (годами жизни которого принято считать 570-490 гг. до н. э.) использовал алгебраические методы, чтобы находить пифагоровы тройки. Однако Прокл писал между 410 и 485 гг. н. э. Томас Литтл Хит считал, что не существует явного упоминания, относящегося к периоду продолжительностью 5 веков после смерти Пифагора, что Пифагор был автором теоремы. Однако, когда авторы, такие как Плутарх и Цицерон, пишут о теореме Пифагора, они пишут так, как будто авторство Пифагора было широко известным и несомненным.«Принадлежит ли эта формула лично перу Пифагора…, но мы можем уверенно считать, что она принадлежит древнейшему периоду пифагорейской математики ».По преданию, Пифагор отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков. Приблизительно в 400 г. до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Приблизительно в 300 г. до н. э. в « Началах» Евклида появилось старейшее аксиоматический доказательство теоремы Пифагора.

Формулировки: Геометрическая формулировка: Изначально теорема была сформулирована следующим образом: В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Алгебраическая формулировка: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. То есть, обозначив длину гипотенузы треугольника через, а длины катетов через a и b: a2+b2=c2 Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.

Доказательства На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии. Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений).

Через подобные треугольники Следующее доказательство алгебраической формулировки - наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры. Пусть ABC есть прямоугольный треугольник с прямым углом C . Проведём высоту из C и обозначим её основание через H . Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC . Введя обозначения получаем Что эквивалентно Сложив, получаем или, что и требовалось доказать

Доказательства методом площадей Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора Доказательство через равнодополняемость Расположим четыре равных прямоугольных треугольника так, как показано на рисунке 1. Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол - 180°. Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата. Что и требовалось доказать. .

Доказательство Евклида Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны. Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника - BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах. Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK. Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK. Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, - это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно: треугольники равны по двум сторонам и углу между ними. Именно - AB=AK, AD=AC - равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата - 90°). Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично. Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах. Идея данного доказательства дополнительно проиллюстрирована с помощью анимации, расположенной выше. Данное доказательство также получило название «Пифагоровы штаны».

Доказательство Леонардо да Винчи Главные элементы доказательства - симметрия и движение. Рассмотрим чертёж, как видно из симметрии, отрезок рассекает квадрат на две одинаковые части (так как треугольники и равны по построению). Пользуясь поворотом на 90 градусов против часовой стрелки вокруг точки, мы усматриваем равенство заштрихованных фигур и. Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей маленьких квадратов (построенных на катетах) и площади исходного треугольника. С другой стороны, она равна половине площади большого квадрата (построенного на гипотенузе) плюс площадь исходного треугольника. Таким образом, половина суммы площадей маленьких квадратов равна половине площади большого квадрата, а следовательно сумма площадей квадратов, построенных на катетах равна площади квадрата, построенного на гипотенузе.

Значение теоремы Пифагора Теорема Пифагора – одна из главных и, можно сказать, самая главная теорема геометрии. Значение её состоит в том, что из неё или с помощью можно вывести большинство теорем геометрии.

Спасибо за внимание!

Строительство

Великие полководцы великой отечественной войны

Крыша

Трагическая смерть георга рихмана

Крыша

Классическая окрошка - рецепт

Новое на сайте

Как приготовить свинину в сметанном соусе Приготовить мясо со сметаной на сковороде

Хеджирование валютных рисков – это будущее

К чему снится признание по соннику

Видео: «стояние зои» - что это было

Как правильно посадить денежное дерево, чтобы водились деньги Вазон денежное дерево

>

Самое популярное

Тема урока: «Явление самоиндукции

Белоснежный торт с ананасами Ананасовая начинка для торта

Клаб сэндвич с тунцом и яйцом

История крестного знамения в христианской церкви

Репетиторы из вуза мгли международный гуманитарно-лингвистический институт Международный гуманитарный лингвистический институт